Imagine a triangle.
Let’s divide the angle at point A in half.
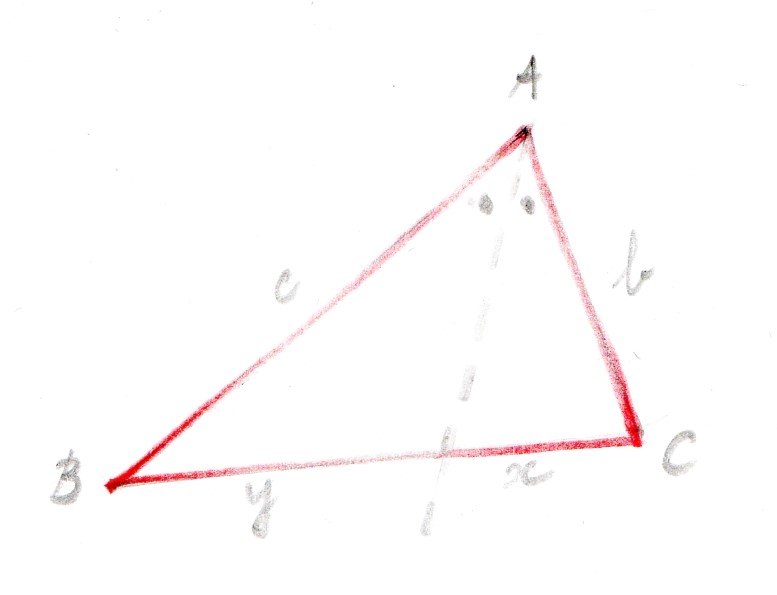
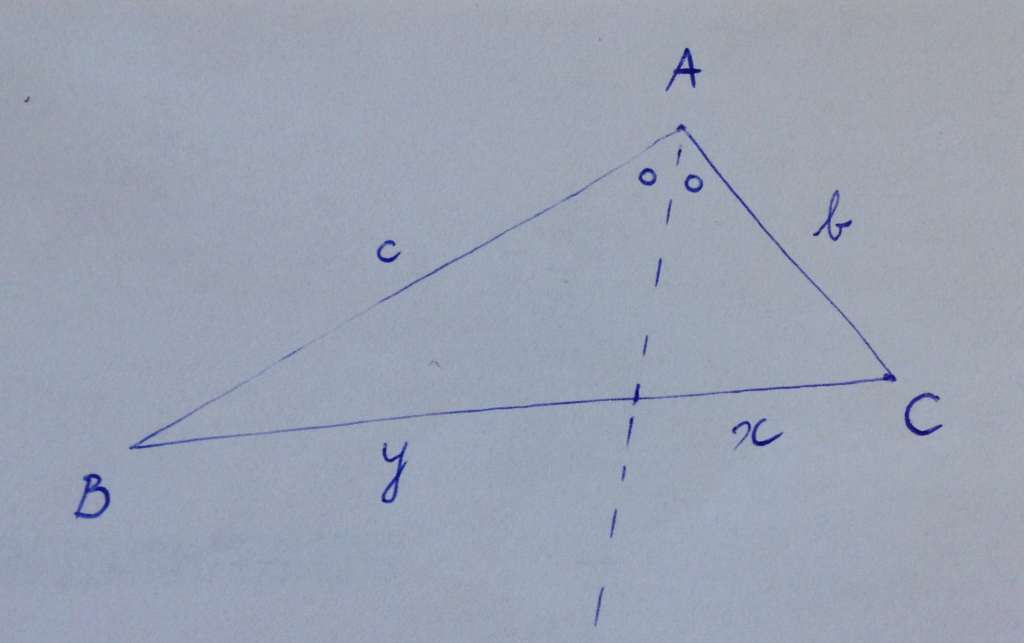
The dotted line is called the bisector. The bisector divides the opposite line segment in a part of length x and a part of length y.
Equal ratios
The Angle Bisector Theorem states that the ratio x : b equals the ratio y : c. Or equivalently, b/x = c/y. This means that if b is for example twice the length of x, then c is twice the length of y.
In the drawing below, measuring in millimeters, I found b/x = 32/25 (= 1.28), while c/y = 61/48, which is roughly1.27. So my drawing is not so bad in that respect.
Who needs proof?
Several proofs of this theorem exist. My interest however is to find a construction that makes immediately clear that the theorem holds. I just want to see that it is true. And from there, effortlessly I hope, write down the proof if anyone needs it.
First attempt: Pairs of congruent triangles
Use compass and ruler (if you like) to construct points P, Q and R.
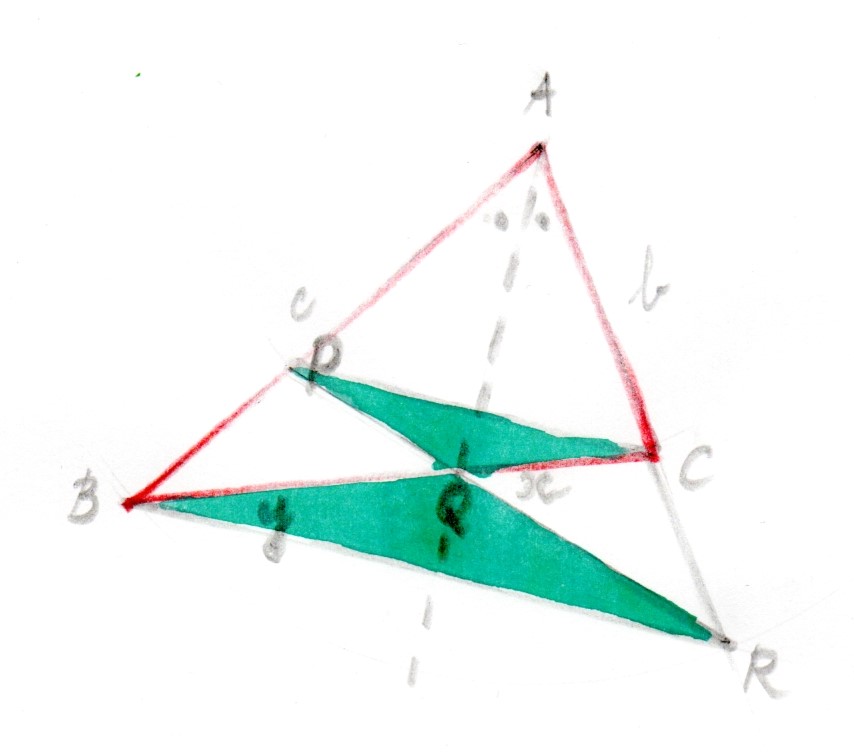
There are two pairs of congruent triangles: △ABR (the large triangle containing all geometry) to △APC (the little one crouching at the top) and △PCQ to △RBQ (the green ones). From these it follows that x : y = PC : BR = b : c.
So x : b = y : c.
It’s not complicated, but it requires too many steps. I would like something simpler.
Second attempt: One congruency less
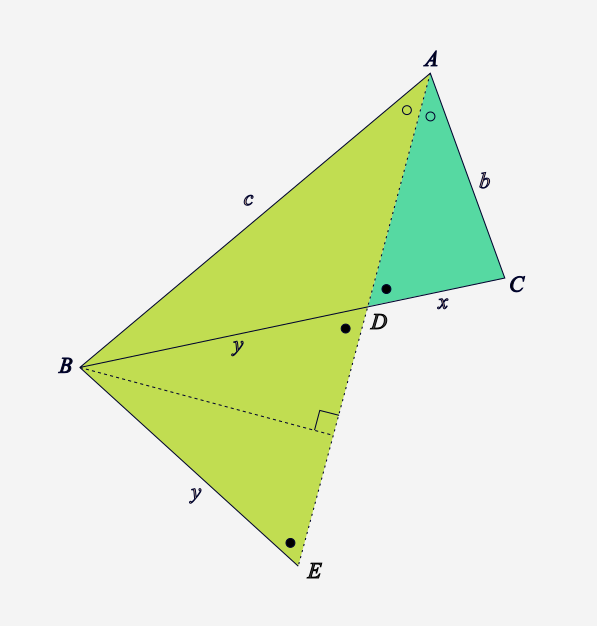
Another possibility is to extend △ABD with the isosceles triangle △BDE as above. The two coloured triangles have two angles in common (indicated with open and closed discs) and so are congruent.
So now we have congruent triangles with x and b in one triangle and y and c in the other. Now it’s obvious that x : b = y : c.
Third attempt: Simpler congruency
Here’s another, even simpler one, arriving at two triangles with two equal angles, therefor congruent.
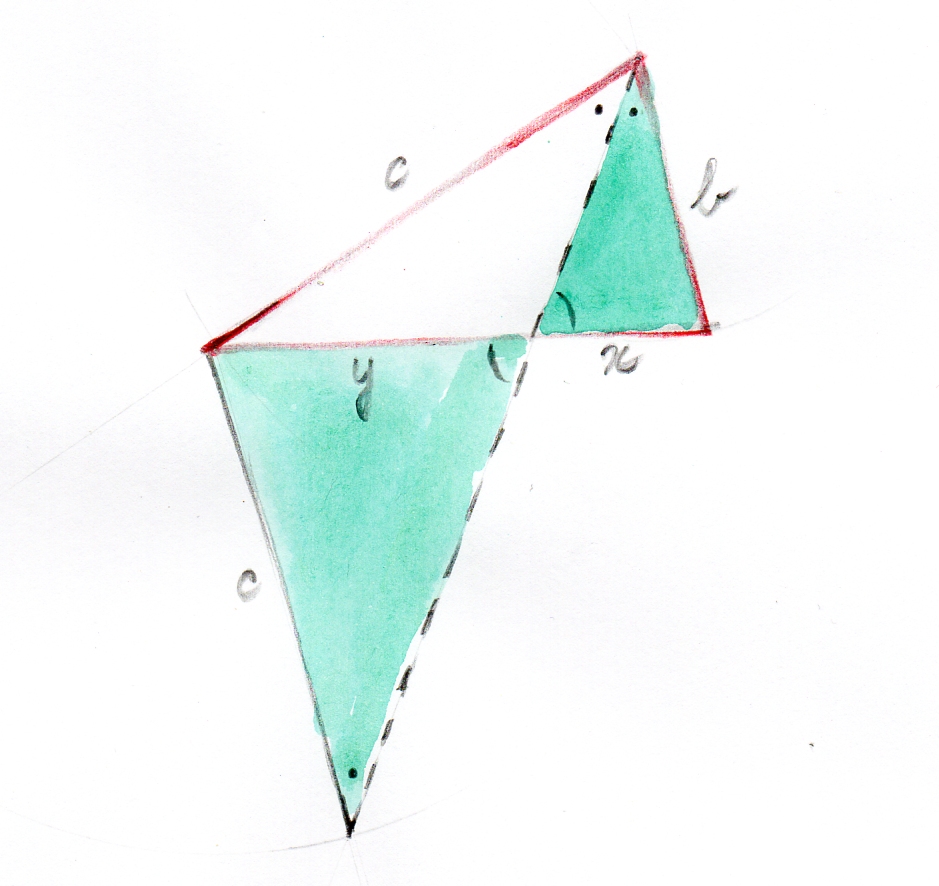
We got rid of the reflection. The congruency consists of a scaling and a rotation operation only.
Final attempt
In the previous attempt it appeared the reflection part of the congruency wasn’t needed. Well, the rotation isn’t needed either:
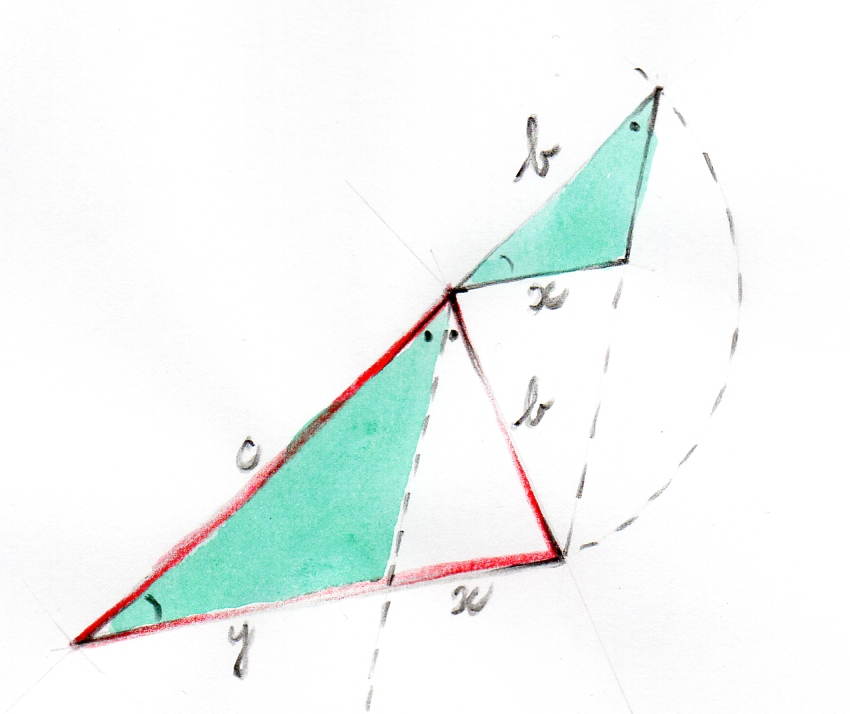
No rotation or reflection, just a scaled (and perhaps translated – depends on the transformation origin) copy.
And the winner is…
I’m satisfied with that, but if you find alternatives, please let me know! Actually, I think my preference goes to attempt number 3.